Forståelse av Grunnleggende Pumpekraft
Å beregne den nødvendige kraften for en pumpe er avgjørende for å sikre effektiv drift og unngå energisløsing. En underdimensjonert pumpe vil ikke levere tilstrekkelig flow eller trykk, mens en overdimensjonert pumpe vil bruke unødvendig mye energi. Denne artikkelen gir deg en detaljert oversikt over hvordan du utfører nøyaktige pumpekraftberegninger.
Den Fundamentale Formelen for Pumpekraft
Den grunnleggende formelen for å beregne hydraulisk pumpekraft (også kjent som væskekraft) er som følger:
$P_{hydraulisk} = \frac{Q \cdot \Delta P}{\eta_{hydraulisk}}$
Hvor:
- $P_{hydraulisk}$ er den hydrauliske kraften i watt (W).
- $Q$ er volumstrømmen (flow rate) i kubikkmeter per sekund ($m^3/s$).
- $\Delta P$ er trykkdifferansen (trykkhodet) over pumpen i pascal (Pa).
- $\eta_{hydraulisk}$ er den hydrauliske virkningsgraden (mellom 0 og 1).
For praktiske beregninger, spesielt når man jobber med liter per minutt (lpm) og bar, kan det være nyttig å konvertere enhetene. Husk at 1 $m^3/s$ = 60 000 lpm og 1 bar = 100 000 Pa.

Elektrisk Pumpekraft
I tillegg til den hydrauliske kraften, er det viktig å vurdere den elektriske kraften som motoren trekker for å drive pumpen. Denne tar hensyn til motorens og pumpens mekaniske virkningsgrad:
$P_{elektrisk} = \frac{P_{hydraulisk}}{\eta_{mekanisk} \cdot \eta_{motor}} = \frac{Q \cdot \Delta P}{\eta_{totalt}}$
Hvor:
- $P_{elektrisk}$ er den elektriske kraften i watt (W).
- $\eta_{mekanisk}$ er den mekaniske virkningsgraden til pumpen (mellom 0 og 1).
- $\eta_{motor}$ er den elektriske virkningsgraden til motoren (mellom 0 og 1).
- $\eta_{totalt}$ er den totale virkningsgraden ($\eta_{hydraulisk} \cdot \eta_{mekanisk} \cdot \eta_{motor}$).
Produsentens datablad for pumpen og motoren vil inneholde informasjon om de ulike virkningsgradene. Det er essensielt å bruke korrekte verdier for å få en nøyaktig beregning av det totale kraftbehovet.
Faktorer som Påvirker Pumpekraftbehovet
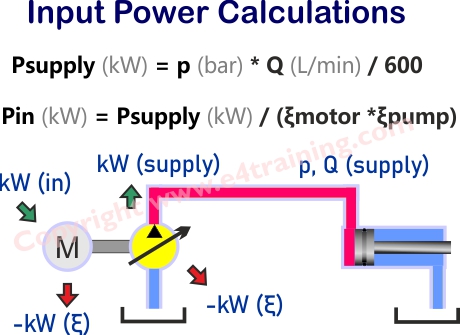
Flere faktorer spiller inn når man skal bestemme kraftbehovet til en pumpe:
- Volumstrøm (Q): Mengden væske som pumpes per tidsenhet. Høyere flow krever mer kraft.
- Trykkdifferanse ($\Delta P$): Forskjellen i trykk mellom pumpens innløp og utløp. Dette inkluderer statisk løftehøyde, trykktap i rør og utstyr, og ønsket utløpstrykk.
- Væskens tetthet ($\rho$): Tyngre væsker krever mer kraft å flytte. Vann har en tetthet på ca. 1000 kg/$m^3$, mens andre væsker kan ha betydelig forskjellig tetthet. Selv om tettheten ikke er direkte i den enkleste formelen over, er den implisitt i beregningen av trykkhodet.
- Viskositet ($\mu$): Tykkere væsker har høyere viskositet og skaper mer friksjon i rørene, noe som øker trykktapet og dermed kraftbehovet.
- Høyde og avstand: Jo høyere væsken må løftes og jo lengre den må transporteres, desto større blir trykktapet på grunn av gravitasjon og friksjon.
- Rørsystemets utforming: Diameteren på rørene, antall bend og ventiler påvirker trykktapet i systemet. Smalere rør og flere hindringer fører til høyere trykktap.
- Pumpens og motorens virkningsgrad ($\eta$): En pumpe og motor med høyere virkningsgrad vil kreve mindre elektrisk kraft for å levere den nødvendige hydrauliske kraften.
Detaljert Blikk på Trykkdifferansen ($\Delta P$)
Nøyaktig bestemmelse av trykkdifferansen er kritisk for korrekt pumpekraftberegning. Trykkdifferansen består av flere komponenter:

- Statisk løftehøyde ($H_s$): Den vertikale avstanden mellom væskenivået på sugesiden og utløpssiden.
- Trykktap i sugeledningen ($h_f,_{suge}$): Friksjonstap i rørene, bend og ventiler på sugesiden.
- Trykktap i trykkledningen ($h_f,_{trykk}$): Friksjonstap i rørene, bend og ventiler på trykksiden.
- Ønsket trykk ved utløpet ($P_{ut}$): Hvis væsken skal leveres med et visst trykk ved enden av rørsystemet.
- Trykkforskjell i beholdere ($\Delta P_{beholder}$): Hvis det er trykkforskjell mellom suge- og utløpsbeholderen.
Den totale trykkdifferansen kan da uttrykkes som:
$\Delta P = \rho \cdot g \cdot H_s + \Delta P_{beholder} + (\sum h_f,_{suge} + \sum h_f,_{trykk}) \cdot \rho \cdot g + P_{ut}$
Hvor $g$ er tyngdeakselerasjonen (ca. 9.81 m/$s^2$). Beregning av friksjonstap ($h_f$) krever kunnskap om rørmateriale, diameter, lengde, flowrate og væskens viskositet (Darcys lov eller Hazen-Williams formel kan brukes).
Praktiske Eksempler på Pumpekraftberegning
La oss se på et enkelt eksempel:
Anta at vi skal pumpe vann (tetthet ca. 1000 kg/$m^3$) med en flowrate på 0.1 $m^3/s$ (6000 lpm) til en høyde på 10 meter. Det er minimalt med trykktap i rørene, og vi ønsker et utløpstrykk på 2 bar (200 000 Pa). Pumpens hydrauliske virkningsgrad er 0.8.
- Statisk løftehøyde: $H_s = 10$ m
- Trykktap: Antas å være neglisjerbart i dette eksempelet.
- Ønsket utløpstrykk: $P_{ut} = 200 000$ Pa
- Trykkdifferanse: $\Delta P = \rho \cdot g \cdot H_s + P_{ut} = 1000 \cdot 9.81 \cdot 10 + 200 000 = 98100 + 200000 = 298100$ Pa
- Hydraulisk kraft: $P_{hydraulisk} = \frac{Q \cdot \Delta P}{\eta_{hydraulisk}} = \frac{0.1 \cdot 298100}{0.8} = 37262.5$ W (ca. 37.3 kW)

Hvis pumpens mekaniske virkningsgrad er 0.9 og motorens virkningsgrad er 0.92, blir den elektriske kraften:
$P_{elektrisk} = \frac{37262.5}{0.9 \cdot 0.92} = \frac{37262.5}{0.828} \approx 45003$ W (ca. 45 kW)
Dette eksempelet illustrerer viktigheten av å inkludere alle relevante faktorer for å estimere det faktiske kraftbehovet.
Viktigheten av Korrekt Pumpevalg Basert på Kraftberegning
Nøyaktig pumpekraftberegning er avgjørende for å velge riktig pumpe for en gitt applikasjon. En korrekt dimensjonert pumpe sikrer:
- Optimal ytelse: Leverer ønsket flow og trykk ved driftspunktet.
- Energieffektivitet: Unngår unødvendig energiforbruk og reduserer driftskostnader.
- Lang levetid: Drift innenfor pumpens spesifikasjoner reduserer slitasje og forlenger levetiden.
- Pålitelig drift: Minimerer risikoen for driftsstans på grunn av overbelastning eller utilstrekkelig kapasitet.

Ved valg av pumpe bør man også vurdere pumpens arbeidspunkt (sammenhengen mellom flow og trykk) og sørge for at det ønskede driftspunktet ligger innenfor pumpens effektive område.
Ytterligere Betraktninger ved Pumpekraftberegning
- Sikkerhetsmargin: Det kan være lurt å legge inn en liten sikkerhetsmargin i beregningene for å kompensere for usikkerheter eller fremtidige endringer i systemet.
- Væskeegenskaper: For ikke-newtonske væsker eller væsker med partikler kan kraftberegningene være mer komplekse og kreve spesialisert kunnskap.
- Driftsforhold: Intermitterende drift eller varierende belastning kan påvirke det gjennomsnittlige kraftforbruket.
- Frekvensomformer: Bruk av frekvensomformer kan tillate justering av pumpehastigheten og dermed tilpasse flow og trykk til behovet, noe som kan føre til betydelige energibesparelser.
Konklusjon: Mestring av Pumpekraftberegning for Effektiv Drift

Grundig forståelse og nøyaktig utførelse av pumpekraftberegninger er fundamentalt for å oppnå effektiv og pålitelig pumpedrift. Ved å ta hensyn til alle relevante faktorer, fra grunnleggende formler til detaljerte trykktapsberegninger og virkningsgrader, kan du sikre at du velger riktig pumpe for din spesifikke applikasjon og optimaliserer energiforbruket. Denne omfattende guiden har gitt deg et solid grunnlag for å mestre kunsten av pumpekraftberegning.